Decision Market Arbitrage

Ever wondered how to profit from inefficient futarchy markets? Here's a simple guide to arbitraging decision markets — a mechanism that's still new enough to have simple alpha.
What is futarchy?
This post by Vitalik is my favorite resource and offers a good in-depth analysis of the mechanism (including a quick overview of potential issues). futarchy.guide is a pretty cool visualization for @MetaDAOProject if you aren't familiar with the conditional vault/AMM architecture.
Opportunity #1: When spot price > both pass and fail markets
For simplicity, let's say a decision market for a proposal is being run for @zcombinatorio (with $ZC as the base token and $SOL as the quote token). Spot is trading 1.75 $SOL per $ZC and the conditional markets are trading at 1.25 and 0.75.
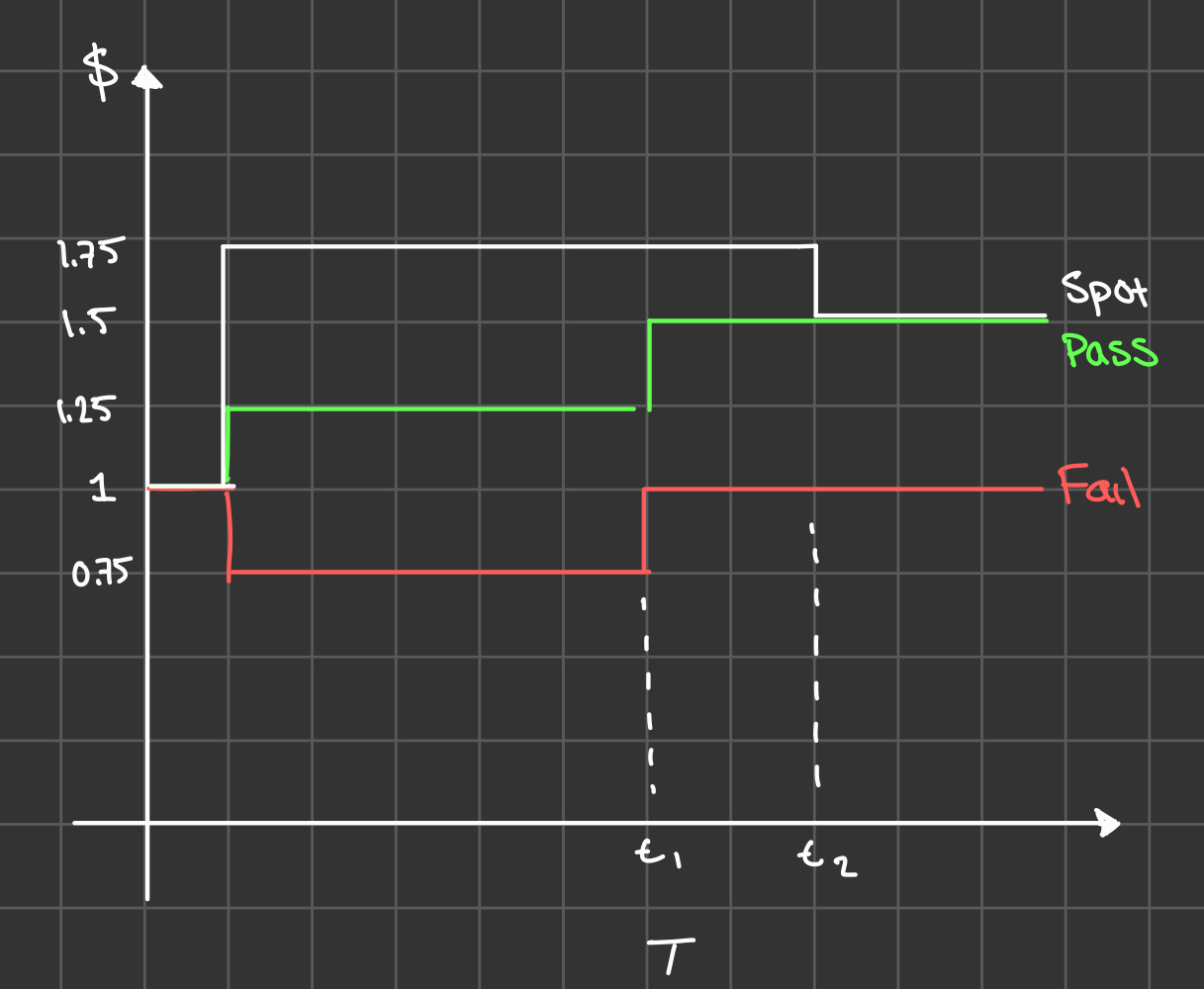
You can:
- Split $SOL into $pSOL and $fSOL (conditional tokens)
- Swap these conditional SOL tokens for conditional $ZC tokens in both markets
- Merge your conditional $ZC back into regular $ZC
- Sell the $ZC into $SOL on the spot market for profit
Through this, you basically buy $ZC in the conditional markets and sell it at a higher price in spot. You can do this until price impact equals the price difference (excluding fees).
Assuming no slippage, if you entered with 1 SOL, you can swap into 1.33 $fZC (1/0.75) in the fail conditional market and 0.8 $pZC (1/1.25) in the pass conditional market. After you merge your conditional $ZC, you'll have min{1.33, 0.8} = 0.8 $ZC total. You can then sell this $ZC for 1.4 $SOL (0.8*1.75). So you would have made a risk-free 40%!
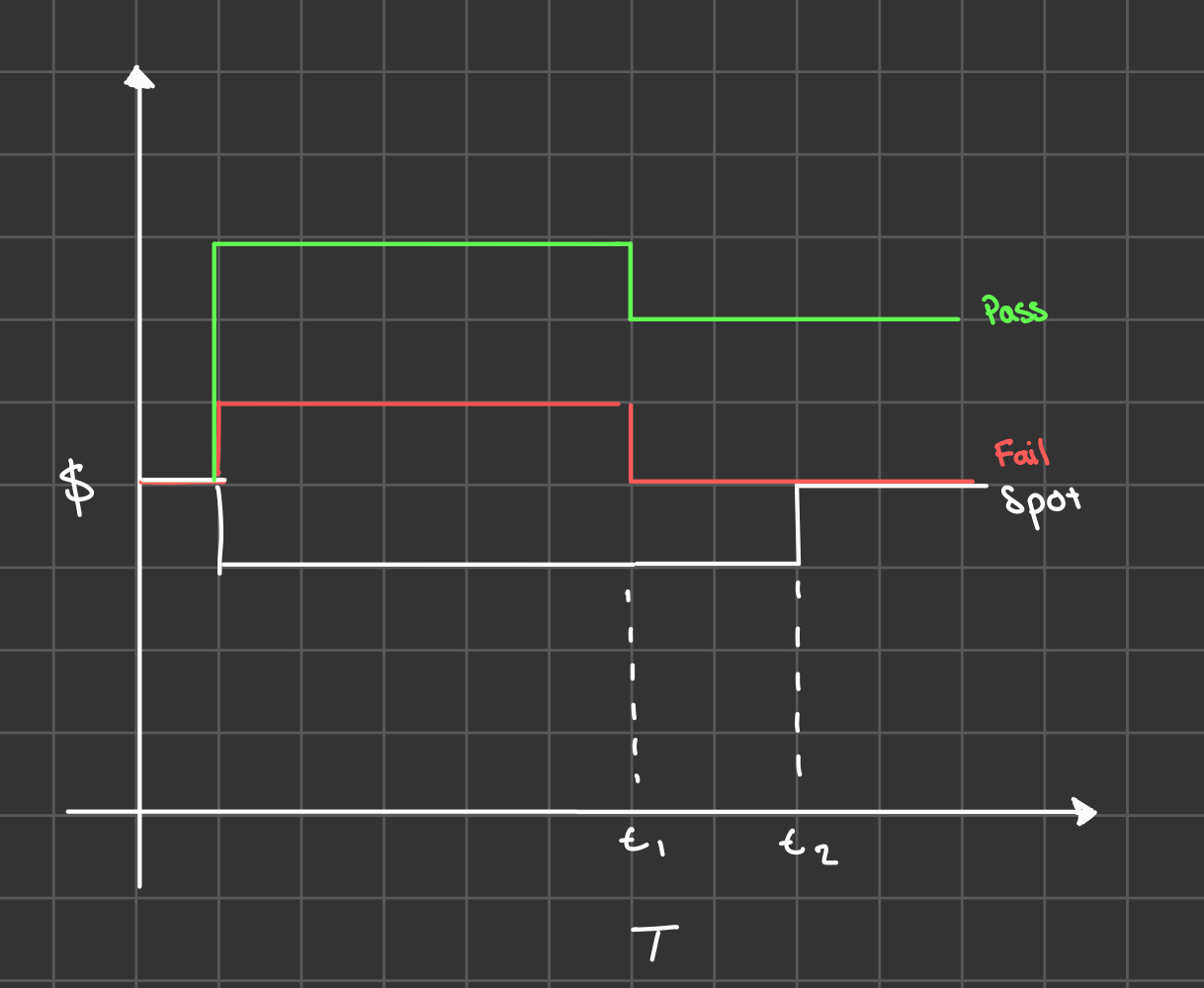
Opportunity #2: When spot price < both pass and fail markets
The reverse works too - buy spot $ZC, split it, swap for conditional $SOL in both markets, then merge.
The Key Insight
No arbitrage exists when spot trades between pass and fail prices.
This is how the mechanism was designed to work - efficient decision markets should always trade the conditional markets between spot.
Think about it: Why would the current price be lower than BOTH the pass scenario AND the fail scenario? Why should it be higher than both?
Caveats
In the math for the above example, I avoided slippage. In the graphs, the price impact for all trades is pretty similar.
In reality, the LP for the conditional markets will probably be less than that of spot. In fact, a common method to fund decision markets is to share liquidity between the spot and the conditional markets. This means that the conditional markets will just have a fraction of the LP of the spot pool.
As such, the price impact for trading the conditional markets will be far greater than for spot, and perceived arbs are most likely smaller in execution.
Current Implementations
@_futarchy has their "Futarchy Solver" on Ethereum, and @MetaDAOProject recently released "Futarchy AMM" on Solana. Both arbitrage automatically per-swap.
@percentmarkets hasn't implemented this yet, so manual arb opportunities still exist.
See you in the dark forest.
- ← Previous
An Ideal World Approximator - Next →
Modes of Operation